↑

Properties

Label 2-297-11.9-c1-0-9
Degree 22
Conductor 297297
Sign 0.977+0.209i0.977 + 0.209i
Analytic cond. 2.371552.37155
Root an. cond. 1.539981.53998
Motivic weight 11
Arithmetic yes
Rational no
Primitive yes
Self-dual no
Analytic rank 00

Origins

Related objects

Downloads

Learn more

Normalization:  

Dirichlet series

L(s)  = 1  + (−0.760 + 2.33i)2-s + (−3.27 − 2.38i)4-s + (−0.305 − 0.941i)5-s + (−3.49 − 2.54i)7-s + (4.08 − 2.96i)8-s + 2.43·10-s + (2.79 + 1.79i)11-s + (1.11 − 3.44i)13-s + (8.60 − 6.25i)14-s + (1.33 + 4.11i)16-s + (−0.816 − 2.51i)17-s + (3.09 − 2.24i)19-s + (−1.23 + 3.81i)20-s + (−6.31 + 5.16i)22-s − 3.45·23-s + ⋯
L(s)  = 1  + (−0.537 + 1.65i)2-s + (−1.63 − 1.19i)4-s + (−0.136 − 0.420i)5-s + (−1.32 − 0.960i)7-s + (1.44 − 1.04i)8-s + 0.770·10-s + (0.841 + 0.540i)11-s + (0.310 − 0.954i)13-s + (2.29 − 1.67i)14-s + (0.333 + 1.02i)16-s + (−0.197 − 0.609i)17-s + (0.710 − 0.516i)19-s + (−0.277 + 0.853i)20-s + (−1.34 + 1.10i)22-s − 0.719·23-s + ⋯

Functional equation

Λ(s)=(297s/2 ΓC(s) L(s)=((0.977+0.209i) Λ‾(2−s)\begin{aligned}\Lambda(s)=\mathstrut & 297 ^{s/2} \, \Gamma_{\C}(s) \, L(s)\cr =\mathstrut & (0.977 + 0.209i)\, \overline{\Lambda}(2-s) \end{aligned}
Λ(s)=(297s/2 ΓC(s+1/2) L(s)=((0.977+0.209i) Λ‾(1−s)\begin{aligned}\Lambda(s)=\mathstrut & 297 ^{s/2} \, \Gamma_{\C}(s+1/2) \, L(s)\cr =\mathstrut & (0.977 + 0.209i)\, \overline{\Lambda}(1-s) \end{aligned}

Invariants

Degree: 22
Conductor: 297297    =    33⋅113^{3} \cdot 11
Sign: 0.977+0.209i0.977 + 0.209i
Analytic conductor: 2.371552.37155
Root analytic conductor: 1.539981.53998
Motivic weight: 11
Rational: no
Arithmetic: yes
Character: χ297(163,⋅)\chi_{297} (163, \cdot )
Primitive: yes
Self-dual: no
Analytic rank: 00
Selberg data: (2, 297, ( :1/2), 0.977+0.209i)(2,\ 297,\ (\ :1/2),\ 0.977 + 0.209i)

Particular Values

L(1)L(1) ≈\approx 0.550573−0.0582124i0.550573 - 0.0582124i
L(12)L(\frac12) ≈\approx 0.550573−0.0582124i0.550573 - 0.0582124i
L(32)L(\frac{3}{2}) not available
L(1)L(1) not available

Euler product

   L(s)=∏pFp(p−s)−1L(s) = \displaystyle \prod_{p} F_p(p^{-s})^{-1}
ppFp(T)F_p(T)
bad3 1 1
11 1+(−2.79−1.79i)T 1 + (-2.79 - 1.79i)T
good2 1+(0.760−2.33i)T+(−1.61−1.17i)T2 1 + (0.760 - 2.33i)T + (-1.61 - 1.17i)T^{2}
5 1+(0.305+0.941i)T+(−4.04+2.93i)T2 1 + (0.305 + 0.941i)T + (-4.04 + 2.93i)T^{2}
7 1+(3.49+2.54i)T+(2.16+6.65i)T2 1 + (3.49 + 2.54i)T + (2.16 + 6.65i)T^{2}
13 1+(−1.11+3.44i)T+(−10.5−7.64i)T2 1 + (-1.11 + 3.44i)T + (-10.5 - 7.64i)T^{2}
17 1+(0.816+2.51i)T+(−13.7+9.99i)T2 1 + (0.816 + 2.51i)T + (-13.7 + 9.99i)T^{2}
19 1+(−3.09+2.24i)T+(5.87−18.0i)T2 1 + (-3.09 + 2.24i)T + (5.87 - 18.0i)T^{2}
23 1+3.45T+23T2 1 + 3.45T + 23T^{2}
29 1+(8.43+6.12i)T+(8.96+27.5i)T2 1 + (8.43 + 6.12i)T + (8.96 + 27.5i)T^{2}
31 1+(0.521−1.60i)T+(−25.0−18.2i)T2 1 + (0.521 - 1.60i)T + (-25.0 - 18.2i)T^{2}
37 1+(2.61+1.90i)T+(11.4+35.1i)T2 1 + (2.61 + 1.90i)T + (11.4 + 35.1i)T^{2}
41 1+(9.63−6.99i)T+(12.6−38.9i)T2 1 + (9.63 - 6.99i)T + (12.6 - 38.9i)T^{2}
43 1+2.12T+43T2 1 + 2.12T + 43T^{2}
47 1+(−3.47+2.52i)T+(14.5−44.6i)T2 1 + (-3.47 + 2.52i)T + (14.5 - 44.6i)T^{2}
53 1+(−2.93+9.01i)T+(−42.8−31.1i)T2 1 + (-2.93 + 9.01i)T + (-42.8 - 31.1i)T^{2}
59 1+(−5.23−3.80i)T+(18.2+56.1i)T2 1 + (-5.23 - 3.80i)T + (18.2 + 56.1i)T^{2}
61 1+(1.48+4.57i)T+(−49.3+35.8i)T2 1 + (1.48 + 4.57i)T + (-49.3 + 35.8i)T^{2}
67 1−0.854T+67T2 1 - 0.854T + 67T^{2}
71 1+(−1.16−3.59i)T+(−57.4+41.7i)T2 1 + (-1.16 - 3.59i)T + (-57.4 + 41.7i)T^{2}
73 1+(9.22+6.70i)T+(22.5+69.4i)T2 1 + (9.22 + 6.70i)T + (22.5 + 69.4i)T^{2}
79 1+(−1.89+5.84i)T+(−63.9−46.4i)T2 1 + (-1.89 + 5.84i)T + (-63.9 - 46.4i)T^{2}
83 1+(1.03+3.19i)T+(−67.1+48.7i)T2 1 + (1.03 + 3.19i)T + (-67.1 + 48.7i)T^{2}
89 1−13.2T+89T2 1 - 13.2T + 89T^{2}
97 1+(0.114−0.353i)T+(−78.4−57.0i)T2 1 + (0.114 - 0.353i)T + (-78.4 - 57.0i)T^{2}
show more
show less
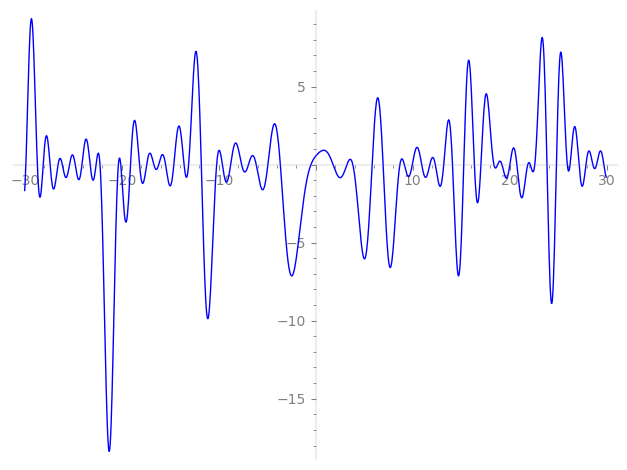
   L(s)=∏p ∏j=12(1−αj,p p−s)−1L(s) = \displaystyle\prod_p \ \prod_{j=1}^{2} (1 - \alpha_{j,p}\, p^{-s})^{-1}

Imaginary part of the first few zeros on the critical line

−11.79352980579389799819635931742, −10.21279980881927434431787373295, −9.620055280831698403154925274866, −8.769957324861384373500141217039, −7.63803551986965951900322125875, −6.93420208250645759408920024757, −6.13255857268088504547818583329, −4.93176813650560240501840717571, −3.64655979471249254612830349645, −0.49843646682302213205710900217, 1.79042180123302417045234622418, 3.21274937553011830155026481865, 3.82586125915300107957783556189, 5.81129469778722963632286510019, 6.94585647552529873539542260642, 8.674116902556386504263998433233, 9.136825690705868354432325332636, 9.957639111193382433775397615698, 10.92703046267470928767276170499, 11.76041003449640865477771633665

Graph of the ZZ-function along the critical line