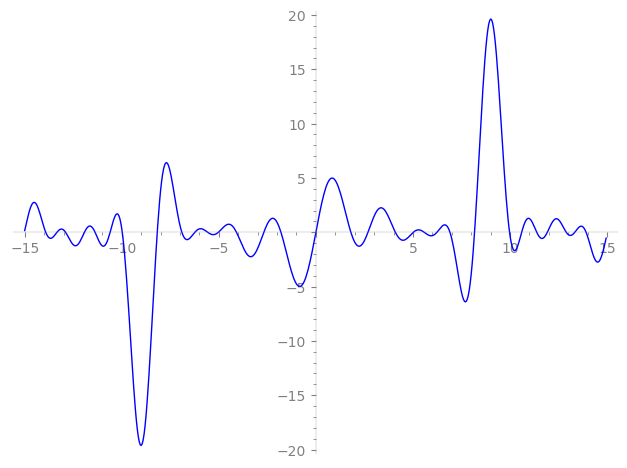
| L(s) = 1 | + 10.5·2-s − 20.9·3-s + 79.2·4-s + 47.3·5-s − 220.·6-s + 497.·8-s + 195.·9-s + 499.·10-s − 565.·11-s − 1.65e3·12-s + 169·13-s − 990.·15-s + 2.71e3·16-s − 1.58e3·17-s + 2.05e3·18-s + 122.·19-s + 3.74e3·20-s − 5.96e3·22-s − 3.58e3·23-s − 1.04e4·24-s − 884.·25-s + 1.78e3·26-s + 998.·27-s + 281.·29-s − 1.04e4·30-s − 1.09e3·31-s + 1.27e4·32-s + ⋯ |
| L(s) = 1 | + 1.86·2-s − 1.34·3-s + 2.47·4-s + 0.846·5-s − 2.50·6-s + 2.75·8-s + 0.803·9-s + 1.57·10-s − 1.40·11-s − 3.32·12-s + 0.277·13-s − 1.13·15-s + 2.65·16-s − 1.33·17-s + 1.49·18-s + 0.0778·19-s + 2.09·20-s − 2.62·22-s − 1.41·23-s − 3.69·24-s − 0.283·25-s + 0.517·26-s + 0.263·27-s + 0.0620·29-s − 2.11·30-s − 0.203·31-s + 2.19·32-s + ⋯ |
\[\begin{aligned}\Lambda(s)=\mathstrut & 637 ^{s/2} \, \Gamma_{\C}(s) \, L(s)\cr =\mathstrut & -\, \Lambda(6-s) \end{aligned}\]
\[\begin{aligned}\Lambda(s)=\mathstrut & 637 ^{s/2} \, \Gamma_{\C}(s+5/2) \, L(s)\cr =\mathstrut & -\, \Lambda(1-s) \end{aligned}\]
Particular Values
| \(L(3)\) |
\(=\) |
\(0\) |
| \(L(\frac12)\) |
\(=\) |
\(0\) |
| \(L(\frac{7}{2})\) |
|
not available |
| \(L(1)\) |
|
not available |
\(L(s) = \displaystyle \prod_{p} F_p(p^{-s})^{-1} \)
| $p$ | $F_p(T)$ |
|---|
| bad | 7 | \( 1 \) |
| 13 | \( 1 - 169T \) |
| good | 2 | \( 1 - 10.5T + 32T^{2} \) |
| 3 | \( 1 + 20.9T + 243T^{2} \) |
| 5 | \( 1 - 47.3T + 3.12e3T^{2} \) |
| 11 | \( 1 + 565.T + 1.61e5T^{2} \) |
| 17 | \( 1 + 1.58e3T + 1.41e6T^{2} \) |
| 19 | \( 1 - 122.T + 2.47e6T^{2} \) |
| 23 | \( 1 + 3.58e3T + 6.43e6T^{2} \) |
| 29 | \( 1 - 281.T + 2.05e7T^{2} \) |
| 31 | \( 1 + 1.09e3T + 2.86e7T^{2} \) |
| 37 | \( 1 - 1.22e4T + 6.93e7T^{2} \) |
| 41 | \( 1 + 1.84e4T + 1.15e8T^{2} \) |
| 43 | \( 1 + 1.80e4T + 1.47e8T^{2} \) |
| 47 | \( 1 - 1.82e3T + 2.29e8T^{2} \) |
| 53 | \( 1 - 1.64e4T + 4.18e8T^{2} \) |
| 59 | \( 1 + 1.78e4T + 7.14e8T^{2} \) |
| 61 | \( 1 - 4.03e4T + 8.44e8T^{2} \) |
| 67 | \( 1 + 2.56e4T + 1.35e9T^{2} \) |
| 71 | \( 1 - 6.27e4T + 1.80e9T^{2} \) |
| 73 | \( 1 + 1.54e3T + 2.07e9T^{2} \) |
| 79 | \( 1 + 7.55e4T + 3.07e9T^{2} \) |
| 83 | \( 1 + 7.37e4T + 3.93e9T^{2} \) |
| 89 | \( 1 - 7.70e4T + 5.58e9T^{2} \) |
| 97 | \( 1 + 4.74e4T + 8.58e9T^{2} \) |
| show more | |
| show less | |
\(L(s) = \displaystyle\prod_p \ \prod_{j=1}^{2} (1 - \alpha_{j,p}\, p^{-s})^{-1}\)
Imaginary part of the first few zeros on the critical line
−9.974561858615409401355689876112, −8.171834658092508589227505346741, −6.90430848370196576750662429863, −6.23504620276802713004990825801, −5.57707794380427331730329683147, −5.02032475186445727425757367502, −4.09208168916424470071704388349, −2.68212148931437692493896608728, −1.80067057036729556440547782132, 0,
1.80067057036729556440547782132, 2.68212148931437692493896608728, 4.09208168916424470071704388349, 5.02032475186445727425757367502, 5.57707794380427331730329683147, 6.23504620276802713004990825801, 6.90430848370196576750662429863, 8.171834658092508589227505346741, 9.974561858615409401355689876112