↑

Properties

Label 4-92e4-1.1-c1e2-0-1
Degree 44
Conductor 7163929671639296
Sign 11
Analytic cond. 4567.784567.78
Root an. cond. 8.221038.22103
Motivic weight 11
Arithmetic yes
Rational yes
Primitive no
Self-dual yes
Analytic rank 00

Origins

Origins of factors

Downloads

Learn more

Normalization:  

Dirichlet series

L(s)  = 1  − 6·5-s − 4·7-s + 2·13-s − 12·19-s + 17·25-s + 6·29-s + 12·31-s + 24·35-s + 16·37-s + 6·41-s − 4·43-s − 8·47-s + 4·49-s − 2·53-s + 4·59-s + 2·61-s − 12·65-s − 8·67-s + 4·71-s + 6·73-s − 24·79-s − 9·81-s − 4·83-s − 2·89-s − 8·91-s + 72·95-s + 6·97-s + ⋯
L(s)  = 1  − 2.68·5-s − 1.51·7-s + 0.554·13-s − 2.75·19-s + 17/5·25-s + 1.11·29-s + 2.15·31-s + 4.05·35-s + 2.63·37-s + 0.937·41-s − 0.609·43-s − 1.16·47-s + 4/7·49-s − 0.274·53-s + 0.520·59-s + 0.256·61-s − 1.48·65-s − 0.977·67-s + 0.474·71-s + 0.702·73-s − 2.70·79-s − 81-s − 0.439·83-s − 0.211·89-s − 0.838·91-s + 7.38·95-s + 0.609·97-s + ⋯

Functional equation

Λ(s)=(71639296s/2 ΓC(s)2 L(s)=( Λ(2−s)\begin{aligned}\Lambda(s)=\mathstrut & 71639296 ^{s/2} \, \Gamma_{\C}(s)^{2} \, L(s)\cr =\mathstrut & \, \Lambda(2-s) \end{aligned}
Λ(s)=(71639296s/2 ΓC(s+1/2)2 L(s)=( Λ(1−s)\begin{aligned}\Lambda(s)=\mathstrut & 71639296 ^{s/2} \, \Gamma_{\C}(s+1/2)^{2} \, L(s)\cr =\mathstrut & \, \Lambda(1-s) \end{aligned}

Invariants

Degree: 44
Conductor: 7163929671639296    =    28⋅2342^{8} \cdot 23^{4}
Sign: 11
Analytic conductor: 4567.784567.78
Root analytic conductor: 8.221038.22103
Motivic weight: 11
Rational: yes
Arithmetic: yes
Character: Trivial
Primitive: no
Self-dual: yes
Analytic rank: 00
Selberg data: (4, 71639296, ( :1/2,1/2), 1)(4,\ 71639296,\ (\ :1/2, 1/2),\ 1)

Particular Values

L(1)L(1) ≈\approx 0.77929310910.7792931091
L(12)L(\frac12) ≈\approx 0.77929310910.7792931091
L(32)L(\frac{3}{2}) not available
L(1)L(1) not available

Euler product

   L(s)=∏pFp(p−s)−1L(s) = \displaystyle \prod_{p} F_p(p^{-s})^{-1}
ppGal⁡(Fp)\Gal(F_p)Fp(T)F_p(T)
bad2 1 1
23 1 1
good3C22C_2^2 1+p2T4 1 + p^{2} T^{4}
5C2C_2 (1+3T+pT2)2 ( 1 + 3 T + p T^{2} )^{2}
7D4D_{4} 1+4T+12T2+4pT3+p2T4 1 + 4 T + 12 T^{2} + 4 p T^{3} + p^{2} T^{4}
11C22C_2^2 1+16T2+p2T4 1 + 16 T^{2} + p^{2} T^{4}
13D4D_{4} 1−2T+3T2−2pT3+p2T4 1 - 2 T + 3 T^{2} - 2 p T^{3} + p^{2} T^{4}
17C22C_2^2 1+10T2+p2T4 1 + 10 T^{2} + p^{2} T^{4}
19D4D_{4} 1+12T+68T2+12pT3+p2T4 1 + 12 T + 68 T^{2} + 12 p T^{3} + p^{2} T^{4}
29D4D_{4} 1−6T+43T2−6pT3+p2T4 1 - 6 T + 43 T^{2} - 6 p T^{3} + p^{2} T^{4}
31D4D_{4} 1−12T+74T2−12pT3+p2T4 1 - 12 T + 74 T^{2} - 12 p T^{3} + p^{2} T^{4}
37C2C_2 (1−8T+pT2)2 ( 1 - 8 T + p T^{2} )^{2}
41D4D_{4} 1−6T+67T2−6pT3+p2T4 1 - 6 T + 67 T^{2} - 6 p T^{3} + p^{2} T^{4}
43D4D_{4} 1+4T+66T2+4pT3+p2T4 1 + 4 T + 66 T^{2} + 4 p T^{3} + p^{2} T^{4}
47D4D_{4} 1+8T+104T2+8pT3+p2T4 1 + 8 T + 104 T^{2} + 8 p T^{3} + p^{2} T^{4}
53D4D_{4} 1+2T+11T2+2pT3+p2T4 1 + 2 T + 11 T^{2} + 2 p T^{3} + p^{2} T^{4}
59D4D_{4} 1−4T+68T2−4pT3+p2T4 1 - 4 T + 68 T^{2} - 4 p T^{3} + p^{2} T^{4}
61D4D_{4} 1−2T+99T2−2pT3+p2T4 1 - 2 T + 99 T^{2} - 2 p T^{3} + p^{2} T^{4}
67D4D_{4} 1+8T+54T2+8pT3+p2T4 1 + 8 T + 54 T^{2} + 8 p T^{3} + p^{2} T^{4}
71D4D_{4} 1−4T+140T2−4pT3+p2T4 1 - 4 T + 140 T^{2} - 4 p T^{3} + p^{2} T^{4}
73D4D_{4} 1−6T+131T2−6pT3+p2T4 1 - 6 T + 131 T^{2} - 6 p T^{3} + p^{2} T^{4}
79C2C_2 (1+12T+pT2)2 ( 1 + 12 T + p T^{2} )^{2}
83D4D_{4} 1+4T+146T2+4pT3+p2T4 1 + 4 T + 146 T^{2} + 4 p T^{3} + p^{2} T^{4}
89D4D_{4} 1+2T+83T2+2pT3+p2T4 1 + 2 T + 83 T^{2} + 2 p T^{3} + p^{2} T^{4}
97D4D_{4} 1−6T+179T2−6pT3+p2T4 1 - 6 T + 179 T^{2} - 6 p T^{3} + p^{2} T^{4}
show more
show less
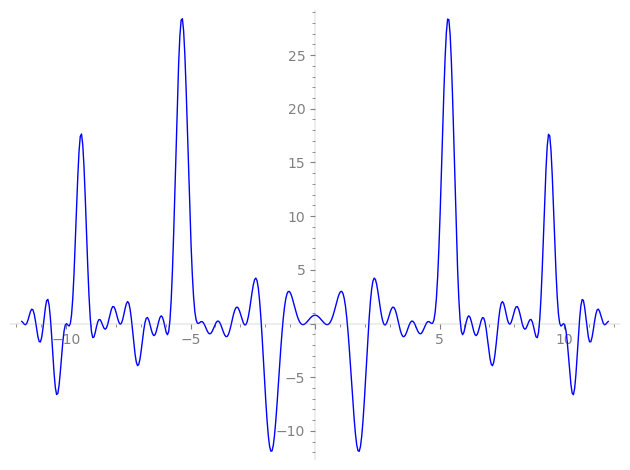
   L(s)=∏p ∏j=14(1−αj,p p−s)−1L(s) = \displaystyle\prod_p \ \prod_{j=1}^{4} (1 - \alpha_{j,p}\, p^{-s})^{-1}

Imaginary part of the first few zeros on the critical line

−7.85111964910540416398113020283, −7.78098523552231746436921124402, −7.35419630103221897974820391213, −6.83541994547435757093443458090, −6.63609082231443004424623561148, −6.29680431745563089588601182998, −6.05573371932215340017507843255, −5.83657206822917314483643711219, −4.69976944413607947119600354203, −4.68850246772116126878247259151, −4.46131312179153461526264297037, −3.99435764542081079557076025353, −3.80485494160127383364013876299, −3.35848250925148638683073740842, −2.86650522883089233885702366067, −2.75243464786618541414837244980, −2.15862349297678166053309177281, −1.29578320510573281359593748324, −0.57114632521050694568744861385, −0.39090756518103539303874738907, 0.39090756518103539303874738907, 0.57114632521050694568744861385, 1.29578320510573281359593748324, 2.15862349297678166053309177281, 2.75243464786618541414837244980, 2.86650522883089233885702366067, 3.35848250925148638683073740842, 3.80485494160127383364013876299, 3.99435764542081079557076025353, 4.46131312179153461526264297037, 4.68850246772116126878247259151, 4.69976944413607947119600354203, 5.83657206822917314483643711219, 6.05573371932215340017507843255, 6.29680431745563089588601182998, 6.63609082231443004424623561148, 6.83541994547435757093443458090, 7.35419630103221897974820391213, 7.78098523552231746436921124402, 7.85111964910540416398113020283

Graph of the ZZ-function along the critical line