↑

Properties

Label 2-30e2-180.119-c1-0-1
Degree 22
Conductor 900900
Sign −0.819+0.573i-0.819 + 0.573i
Analytic cond. 7.186537.18653
Root an. cond. 2.680772.68077
Motivic weight 11
Arithmetic yes
Rational no
Primitive yes
Self-dual no
Analytic rank 00

Origins

Related objects

Downloads

Learn more

Normalization:  

Dirichlet series

L(s)  = 1  + (−1.38 + 0.295i)2-s + (−1.64 − 0.531i)3-s + (1.82 − 0.817i)4-s + (2.43 + 0.247i)6-s + (−2.08 + 3.61i)7-s + (−2.28 + 1.67i)8-s + (2.43 + 1.75i)9-s + (−3.22 + 5.57i)11-s + (−3.44 + 0.378i)12-s + (1.53 − 0.887i)13-s + (1.81 − 5.61i)14-s + (2.66 − 2.98i)16-s + 0.950·17-s + (−3.88 − 1.70i)18-s − 2.19i·19-s + ⋯
L(s)  = 1  + (−0.977 + 0.209i)2-s + (−0.951 − 0.306i)3-s + (0.912 − 0.408i)4-s + (0.994 + 0.101i)6-s + (−0.788 + 1.36i)7-s + (−0.806 + 0.590i)8-s + (0.811 + 0.584i)9-s + (−0.971 + 1.68i)11-s + (−0.994 + 0.109i)12-s + (0.426 − 0.246i)13-s + (0.485 − 1.49i)14-s + (0.665 − 0.746i)16-s + 0.230·17-s + (−0.915 − 0.401i)18-s − 0.503i·19-s + ⋯

Functional equation

Λ(s)=(900s/2 ΓC(s) L(s)=((−0.819+0.573i) Λ‾(2−s)\begin{aligned}\Lambda(s)=\mathstrut & 900 ^{s/2} \, \Gamma_{\C}(s) \, L(s)\cr =\mathstrut & (-0.819 + 0.573i)\, \overline{\Lambda}(2-s) \end{aligned}
Λ(s)=(900s/2 ΓC(s+1/2) L(s)=((−0.819+0.573i) Λ‾(1−s)\begin{aligned}\Lambda(s)=\mathstrut & 900 ^{s/2} \, \Gamma_{\C}(s+1/2) \, L(s)\cr =\mathstrut & (-0.819 + 0.573i)\, \overline{\Lambda}(1-s) \end{aligned}

Invariants

Degree: 22
Conductor: 900900    =    22⋅32⋅522^{2} \cdot 3^{2} \cdot 5^{2}
Sign: −0.819+0.573i-0.819 + 0.573i
Analytic conductor: 7.186537.18653
Root analytic conductor: 2.680772.68077
Motivic weight: 11
Rational: no
Arithmetic: yes
Character: χ900(299,⋅)\chi_{900} (299, \cdot )
Primitive: yes
Self-dual: no
Analytic rank: 00
Selberg data: (2, 900, ( :1/2), −0.819+0.573i)(2,\ 900,\ (\ :1/2),\ -0.819 + 0.573i)

Particular Values

L(1)L(1) ≈\approx 0.0227332−0.0721774i0.0227332 - 0.0721774i
L(12)L(\frac12) ≈\approx 0.0227332−0.0721774i0.0227332 - 0.0721774i
L(32)L(\frac{3}{2}) not available
L(1)L(1) not available

Euler product

   L(s)=∏pFp(p−s)−1L(s) = \displaystyle \prod_{p} F_p(p^{-s})^{-1}
ppFp(T)F_p(T)
bad2 1+(1.38−0.295i)T 1 + (1.38 - 0.295i)T
3 1+(1.64+0.531i)T 1 + (1.64 + 0.531i)T
5 1 1
good7 1+(2.08−3.61i)T+(−3.5−6.06i)T2 1 + (2.08 - 3.61i)T + (-3.5 - 6.06i)T^{2}
11 1+(3.22−5.57i)T+(−5.5−9.52i)T2 1 + (3.22 - 5.57i)T + (-5.5 - 9.52i)T^{2}
13 1+(−1.53+0.887i)T+(6.5−11.2i)T2 1 + (-1.53 + 0.887i)T + (6.5 - 11.2i)T^{2}
17 1−0.950T+17T2 1 - 0.950T + 17T^{2}
19 1+2.19iT−19T2 1 + 2.19iT - 19T^{2}
23 1+(−1.74+1.01i)T+(11.5−19.9i)T2 1 + (-1.74 + 1.01i)T + (11.5 - 19.9i)T^{2}
29 1+(5.65+3.26i)T+(14.5+25.1i)T2 1 + (5.65 + 3.26i)T + (14.5 + 25.1i)T^{2}
31 1+(−2.46+1.42i)T+(15.5−26.8i)T2 1 + (-2.46 + 1.42i)T + (15.5 - 26.8i)T^{2}
37 1−5.83iT−37T2 1 - 5.83iT - 37T^{2}
41 1+(6.16−3.55i)T+(20.5−35.5i)T2 1 + (6.16 - 3.55i)T + (20.5 - 35.5i)T^{2}
43 1+(−2.65+4.59i)T+(−21.5−37.2i)T2 1 + (-2.65 + 4.59i)T + (-21.5 - 37.2i)T^{2}
47 1+(0.349+0.201i)T+(23.5+40.7i)T2 1 + (0.349 + 0.201i)T + (23.5 + 40.7i)T^{2}
53 1+4.87T+53T2 1 + 4.87T + 53T^{2}
59 1+(−1.34−2.32i)T+(−29.5+51.0i)T2 1 + (-1.34 - 2.32i)T + (-29.5 + 51.0i)T^{2}
61 1+(2.04−3.54i)T+(−30.5−52.8i)T2 1 + (2.04 - 3.54i)T + (-30.5 - 52.8i)T^{2}
67 1+(5.44+9.43i)T+(−33.5+58.0i)T2 1 + (5.44 + 9.43i)T + (-33.5 + 58.0i)T^{2}
71 1+2.23T+71T2 1 + 2.23T + 71T^{2}
73 1+1.74iT−73T2 1 + 1.74iT - 73T^{2}
79 1+(0.214+0.123i)T+(39.5+68.4i)T2 1 + (0.214 + 0.123i)T + (39.5 + 68.4i)T^{2}
83 1+(10.1+5.83i)T+(41.5+71.8i)T2 1 + (10.1 + 5.83i)T + (41.5 + 71.8i)T^{2}
89 1+6.13iT−89T2 1 + 6.13iT - 89T^{2}
97 1+(−15.7−9.08i)T+(48.5+84.0i)T2 1 + (-15.7 - 9.08i)T + (48.5 + 84.0i)T^{2}
show more
show less
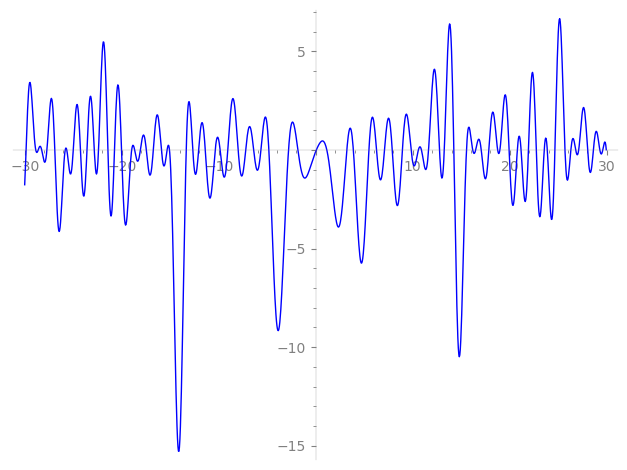
   L(s)=∏p ∏j=12(1−αj,p p−s)−1L(s) = \displaystyle\prod_p \ \prod_{j=1}^{2} (1 - \alpha_{j,p}\, p^{-s})^{-1}

Imaginary part of the first few zeros on the critical line

−10.36265773578019029178792621409, −9.853252984327107190919732442079, −9.064395312540465964366297951978, −7.994905009010870658175189302232, −7.21731104582358157175839459894, −6.39553639295459336010379023433, −5.64950169595843359210450618847, −4.83161989047987755089299683268, −2.80169313632431834242878374529, −1.83485039388050321110250940379, 0.06288348438562582030974291662, 1.14427857683208484313900950333, 3.20596671888702095242000964035, 3.87759972531138006674528060837, 5.48396599439314403067804666702, 6.26880400088140472775013522000, 7.09007382237209152218451003489, 7.88839247246327611809660087927, 8.935646905849912559751750184383, 9.830893479801243539900519193255

Graph of the ZZ-function along the critical line